9058. Серебряная
цепочка
Не время задавать вопросы! В
музее истории в Лондоне находится серебряная цепочка XIX века, принадлежавшая
самой королеве Виктории. Джонни Инглишу придется ее достать, чтобы отдать в
качестве выкупа за секретные документы. Джонни без проблем сможет пробраться в
музей ночью, но похищенную цепочку нужно чем-то заменить, чтобы пропажу не
заметили слишком быстро. У Джонни с собой есть другая цепочка. Он хочет
заменить цепочку в музее на свою.
Цепочка в музее зафиксирована и
представляет собой замкнутую ломаную, звенья которой являются отрезками.
Цепочка Джонни Инглиша, лежащая перед ним на столе, тоже представляет собой
замкнутую ломаную, звенья которой являются отрезками. Джонни интересуется,
сможет ли он закрепить свою цепочку в музее, на месте украденной, так, чтобы
получилась точно такая же ломаная, как та, что образована цепочкой, находящейся
в музее. В том числе, если цепочка в музее покрывает один отрезок несколько
раз, то Джонни хочет чтобы и его цепочка покрывала этот отрезок столько же раз.
Джонни может сгибать свою цепочку в произвольных местах, а не только в концах
звеньев.
Ломаные могут иметь
самопересечения, звенья нулевой длины и накладывающиеся звенья.
Вход. В первой строке дано одно целое
число n (3 ≤ n ≤ 1000) – количество вершин ломаной, представляющей цепочку в музее. В следующих n строках
даны координаты вершин первой ломаной в порядке обхода xi, yi (|xi|, | yi| ≤ 1000). В следующей строке дано
одно целое число m (3 ≤ m ≤ 1000) – количество вершин ломаной, представляющей цепочку Джонни. В следующих m строках
даны координаты вершин второй ломаной в порядке обхода xi, yi (|xi|, | yi|
≤ 1000).
Выход. В единственной строке выведите “Yes”, если Джонни сможет закрепить свою цепочку точно так же, как закреплена
та, что хранится в музее. И “No” иначе.
|
Пример
входа 1 |
Пример
выхода 1 |
|
3 0 0 1 0 0 1 3 1 1 0 1 1 0 |
Yes |
|
|
|
|
Пример
входа 2 |
Пример
выхода 2 |
|
5 0 0 1 0 1 1 1 0 1 1 3 0 0 1 0 1 1 |
No |
РЕШЕНИЕ
геометрия
Анализ алгоритма
Ответ на задачу будет “Yes”, если длины цепочек одинаковы.
Цепочки представляются замкнутыми ломаными. Поэтому достаточно вычислить и
сравнить длины заданных ломаных.
Пусть (xi, yi) – координаты вершин ломаной в порядке обхода (i
= 0, 1, 2, …, n – 1). Установим (xn, yn) = (x0, y0). Тогда длина
замкнутой ломаной равна
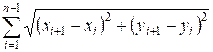
Реализация алгоритма
Объявим
массивы для хранения вершин (xi, yi) ломаных.
#define MAX 1002
double x[MAX], y[MAX];
Читаем
координаты вершин первой цепочки. Установим (xn, yn) = (x0, y0).
scanf("%d", &n);
for (i = 0; i < n; i++)
scanf("%lf %lf", &x[i], &y[i]);
x[n] = x[0]; y[n] =
y[0];
Вычисляем
длину p1 первой цепочки.
p1 = 0;
for (i = 0; i < n; i++)
p1 += sqrt((x[i + 1] - x[i]) * (x[i + 1] -
x[i]) +
(y[i + 1] - y[i]) * (y[i + 1] - y[i]));
Читаем
координаты вершин второй цепочки. Установим (xm, ym) = (x0, y0).
scanf("%d", &m);
for (i = 0; i < m; i++)
scanf("%lf %lf", &x[i],
&y[i]);
x[m] = x[0]; y[m] =
y[0];
Вычисляем
длину p2 второй цепочки.
p2 = 0;
for (i = 0; i < m; i++)
p2 += sqrt((x[i + 1] - x[i]) * (x[i + 1] -
x[i]) +
(y[i + 1] - y[i]) * (y[i + 1] -
y[i]));
Сравниваем
длины цепочек p1 и p2 и выводим ответ.
if (fabs(p1 - p2) < 1e-6) printf("Yes\n");
else printf("No\n");